heap
heap이란 최대값 또는 최소값을 빠르게 찾기 위해서 고안된 트리모양의 자료구조이다.
이진 트리에서 각 노드의 키 값이 그 자식 노드보다 큰 트리를 최대 트리(max tree)라고 하며,
최대 힙(max heap)은 최대 트리의 특성을 만족하는 완전 이진 트리(complete binary tree)이다.
최대 힙의 루트노드에는 트리의 최대값이 저장된다.
최소 트리(min tree)는 각 노드의 값이 그 자식 노드보다 작은 트리이다.
최소 힙(min heap)은 최소 트리이면서 완전 이진 트리 조건을 만족한다.
최소 힙의 로트노드에는 트리의 최소값이 저장된다.
노드 추가
max heap에서 노드 추가하기
알고리즘 과정
- 최대 힙의 마지막 노드 다음에 새로운 노드를 추가한다.
- 새 노드와 그 부모 노드의 크기를 비교하여 새 노드가 더 크다면 부모 노드와 위치를 (swap)한다.
- 새 노드가 올바른 위치를 찾거나 루트에 도달할 때까지 2번을 반복한다.
그림으로 다시 보기
(https://csacademy.com/app/graph_editor/ 사이트를 사용하여 트리를 그림)
: 80을 추가하는 경우
- 초기 설정
현재 리스트 상태
[ 0, 40, 20, 10, 12, 5]
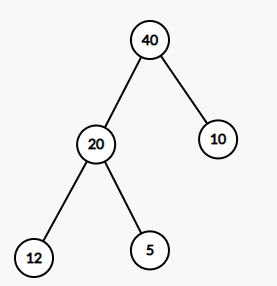
- 마지막 위치에 80 추가
[ 0, 40, 20, 10, 12, 5, 80]
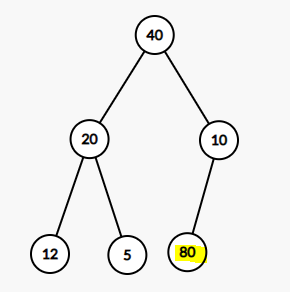
- 80과 10 swap
[ 0, 40, 20, 80, 12, 5, 10]

- 40과 80 swap
[ 0, 80, 20, 40, 12, 5, 10]

min heap에서 노드 추가하기
알고리즘 과정 (max heap에서 크고, 작은 것만 바뀜.)
- 최소 힙의 마지막 노드 다음에 새로운 노드를 추가한다.
- 새 노드와 그 부모 노드의 크기를 비교하여 부모 노드가 더 크다면 위치를 swap한다.
- 새 노드가 올바른 위치를 찾거나 루트에 도달할 때까지 2번을 반복한다.
노드 삭제
max heap의 노드 삭제하기
알고리즘 과정
- 루트 값을 반환할 변수에 복사하고, 마지막 노드를 루트 위치로 이동시킨다.
- 새 루트의 좌우 자식 노드 중 큰 값을 비교 노드로 선택한다.
- 새 루트와 선택한 자식 노드를 비교하여 새 루트가 더 크면 재구성을 종료한다.
- 자식 노드가 새 루트보다 더 크면 교환(swap)하고, 하위 레벨에서 (2)번 과정을 반복한다.
그림으로 다시 보기
- 초기 설정
현재 리스트 상태
[0, 30, 20, 8, 15, 10]
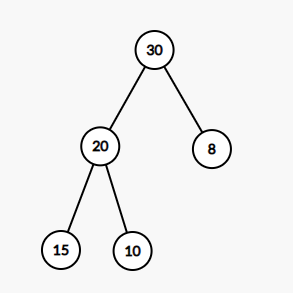
- 루트 값은 반환, 마지막 노드를 루트 위치로 이동.
[0, 10, 20, 8, 15]
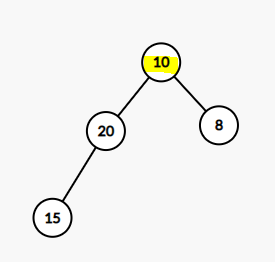
- 좌우 자식 노드 중 큰 값을 가진 노드로 비교 노드 선택 > 왼쪽 노드(20) 선택됨.
- 새 루트와 선택한 자식 노드를 비교 > 자식 노드가 더 크므로 swap함.
[0, 20, 10, 8, 15]
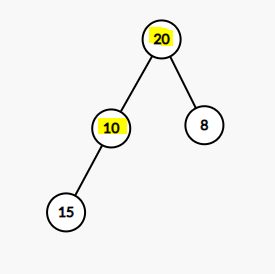
- 자식 노드 15와 10을 비교 > 부모 노드인 10이 더 작으므로 swap
[0, 20, 15, 8, 10]

min heap의 노드 삭제하기
알고리즘 과정 (max heap에서 크고, 작은 것만 바뀜.)
- 루트 값을 반환할 변수에 미리 복사하고, 마지막 노드를 루트 위치로 이동시킨다.
- 새 루트의 좌우 자식 노드 중 작은 값을 비교 노드로 선택한다.
- 새 루트와 선택한 자식 노드를 비교하여 새 루트가 더 작으면 재구성을 종료한다.
- 자식 노드가 새 루트보다 더 작으면 교환(swap)하고, 하위 레벨에서 (2)번 과정을 반복한다.
구현하기
완전 이진 트리를 굳이 만들지 않고, 힙을 배열(리스트)로 나타낸다!
루트 노드부터의 인덱스는 다음과 같은 규칙을 따른다.
- 루트 노드의 인덱스 = 1
- 왼쪽 자식 노드의 인덱스 = 부모 노드의 인덱스 * 2
- 오른쪽 자식 노드의 인덱스 = 부모 노드의 인덱스 * 2 + 1
- 부모 노드의 인덱스 = 자식 노드의 인덱스 // 2
코드로 구현하면 다음과 같다.
-> 여기서는 size가 정해져있는 heap을 전제로 함. size가 정해져 있지 않다면 그냥 isFull()을 확인하지 않고 추가하면 된다.
# 최대 힙에서 노드 추가와 삭제.
class MaxHeap:
def __int__(self, size):
self.size = size
self.heap = [None] * size
self.count = 0 # 현재 노드 수
def __str__(self):
return "Heap, 0 is Dummy "
def add_heap(self, item): # item = 넣을 노드
if self.isFull():
print("reject - full heap")
return
self.count += 1
i = self.count
while i != 1 and item > self.heap[i // 2]: # heap이 비어있는지 확인
self.heap[i] = self.heap[i // 2] # swap
i //= 2 # 위로 이동
self.heap[i] = item
print("%2d" % item)
print(self.heap)
def del_heap(self):
if self.isEmpty():
print("reject - empty heap")
return
item = self.heap[1]
temp = self.heap[self.count] # 마지막 원소 가져옴.
self.heap[self.count] = None
self.count -= 1
parent = 1
child = 2
while child <= self.count:
if child < self.count and self.heap[child] < self.heap[child + 1]: # 좌우 자식 중 큰 자식 선택
child += 1
if temp > self.heap[child]: break # 구성 완료
self.heap[parent] = self.heap[child]
parent = child
child *= 2
if self.count != 0: # 노드가 적어도 2개 있었던 경우 - 1개 였다면 pop하고 끝
self.heap[parent] = temp # 마지막 위치에 temp 저장
return item
def isEmpty(self):
return self.count == 1 # 0번째 원소는 미사용. - 항상 None
def isFull(self):
return self.count == self.size - 1
heapq 모듈
heapq 모듈은 이진 트리 기반의 최소 힙(min heap) 자료구조를 제공한다.
모듈 임포트
import heapq
힙에 원소 추가
- heapq.heappush() 함수를 이용하여 힙에 원소를 추가할 수 있다.
- 시간 복잡도: O(log(n))
import heapq
heap = []
heapq.heappush(heap, 4)
heapq.heappush(heap, 7)
heapq.heappush(heap, 1)
heapq.heappush(heap, 9)
print(heap)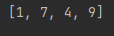
힙에서 원소 삭제
- heapq.heappop() 함수를 이용하여 힙의 원소를 삭제할 수 있다.
- 시간 복잡도: O(log(n))
import heapq
heap = [1, 3, 7, 4]
print(heapq.heappop(heap))
print(heap)
print(heapq.heappop(heap))
print(heap)
최소값 얻기
- 최소값을 삭제하지 않고, 단순히 얻기 위해서는 인덱스에 접근하면 됨.
import heapq
heap = [1, 3, 7, 4]
print(heap[0])
기존 리스트를 힙으로 변환
- heapq.heapify() 함수를 이용하여 기존 리스트를 힙으로 변환할 수 있다.
- 시간 복잡도: O(n)
- 주의할 점
- 새로운 리스트를 반환하는 함수가 아니라, 인자로 넘긴 리스트에 직접 반영함.
- 새로운 리스트가 필요하면 복제 후, 인자로 넘겨야 함.
import heapq
nums = [4, 1, 7, 3, 8, 5]
heap = nums[:] # 복제
heapq.heapify(heap)
print(nums)
print(heap)
[응용] 최대 힙
힙에 튜플(tuple) 원소를 추가, 삭제하면 된다.
각 값에 대한 우선순위를 먼저 구한 뒤, (우선순위, 값) 구조의 튜플 형태로 힙에 추가하거나 삭제하면 된다.
import heapq
nums = [4, 1, 7, 3, 8, 5]
heap = []
for num in nums:
heapq.heappush(heap, (-num, num)) # (우선 순위, 값)
while heap:
print(heapq.heappop(heap)[1]) # index 1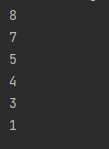
'⌨️ Algorithm > Python' 카테고리의 다른 글
| [Python 문제풀이] 백준 11000번: 강의실 배정 (0) | 2023.01.14 |
|---|---|
| [Python 문제풀이] 백준 2212번: 센서 (0) | 2023.01.14 |
| [Python 문법] 람다(lambda) (0) | 2023.01.12 |
| [Algorithm] Week 2. 그리디 (0) | 2023.01.12 |
| [Algorithm] Week 1. 큐와 스택 (0) | 2023.01.12 |



댓글